1. 개요
픽셀 셰이더(Pixel Shader, PS)는 그래픽스 파이프라인의 프로그래밍 가능 스테이지로, RS로부터 전달받은 개별 프래그먼트(Fragment)에 대해 실행된다.
픽셀 셰이더의 주요 역할은 해당 프래그먼트(보간된 UV, 보간된 Normal, 보간된 월드 위치 등의 데이터가 포함된 픽셀이 될 후보)의 최종 색상(Final Color)을 결정하는 것이다.
이 과정의 대부분은 표면의 재질(Material)과 광원(Light)이 어떻게 상호작용하는지 수학적으로 시뮬레이션하는 조명(Lighting) 계산이 필요하다.
Illumination (조명)
- 조명(또는 음영)은 빛과 물체 간의 상호작용을 다루는 기술을 의미한다. 가장 널리 사용되는 조명 방법은 Phong 모델에 기반을 두고 있으며, 이는 상업용 게임에서 널리 채택되었고, 다양한 고급 조명 기술의 기초가 된다.
Phong 모델
- Phong 모델은 다음 네 가지 항목으로 구성된다
- Diffuse (확산), Specular (반사), Ambient (주변), Emissive (방출)
Light sources

- Point Light (점광원):
- 이는 한 점에서 모든 방향으로 빛을 방출한다.
- 거리에 따라 빛의 Intensity (강도)가 감소한다.
- Directional Light (방향광):
- 이는 하나의 방향에서 Scene을 균일하게 비춘다.
- 거리에 따라 빛의 강도가 변하지 않는다.
- Spotlight (스포트라이트):
- 이는 원뿔 형태의 빛을 만든다.
- 빛의 원뿔과 스포트라이트 소스의 중심에 가까워질수록 강도가 증가한다.
- Ambient (주변광):
- 이는 광원이 없는 경우에도 물체를 비춥니다. (일정한 빛)
- 강도가 완전히 균일하다.
- 그 외에 절두체 모양의 Light Source도 있다.
2. 조명 계산을 위한 입력 데이터
조명 계산은 픽셀 셰이더가 고립되어 수행할 수 없다. 래스터라이저와 CPU로부터 다음과 같은 필수 데이터들을 입력받아야 한다.
2.1. From 래스터라이저 (보간된 데이터)
래스터라이저는 VS 또는 DS가 출력한 정점의 속성 값들을 프래그먼트 위치에 맞게 보간(Interpolate)하여 PS에게 전달한다.
- WorldPosition (월드 공간 위치): 픽셀의 3D 월드 공간 좌표. (광원 벡터, 시야 벡터 계산에 필수)
- Normal (법선 벡터): 표면의 방향. (조명 계산의 가장 핵심이 되는 값)
- TexCoord (UV 좌표): 텍스처 샘플링(알베도, 노멀 맵 등)을 위한 2D 좌표.
- T, B (Tangent, Bitangent): (노멀 매핑 사용 시) 탄젠트 공간(Tangent Space)을 정의하는 벡터.
2.2. From CPU (전역 데이터)
CPU는 렌더링될 씬(Scene)의 전역 정보를 상수 버퍼(Constant Buffer)를 통해 GPU에 전달한다. 픽셀 셰이더는 이 버퍼에 접근하여 다음 정보를 읽는다.
- 광원 정보 (Light Properties):
- 광원의 위치 (World Space)
- 광원의 방향 (World Space)
- 광원의 색상 (Color) 및 강도 (Intensity)
- 카메라 정보 (Camera Properties):
- 카메라(View)의 월드 공간 위치. (스페큘러 계산 시 시선 벡터(View Vector)를 구하기 위해 필요)
- 재질 정보 (Material Properties):
- 표면의 반사율(Albedo), 거칠기(Roughness), 금속성(Metallic) 등. (현대 PBR 셰이딩의 핵심 요소)
3. 표준 조명 모델 (Standard Lighting Model)
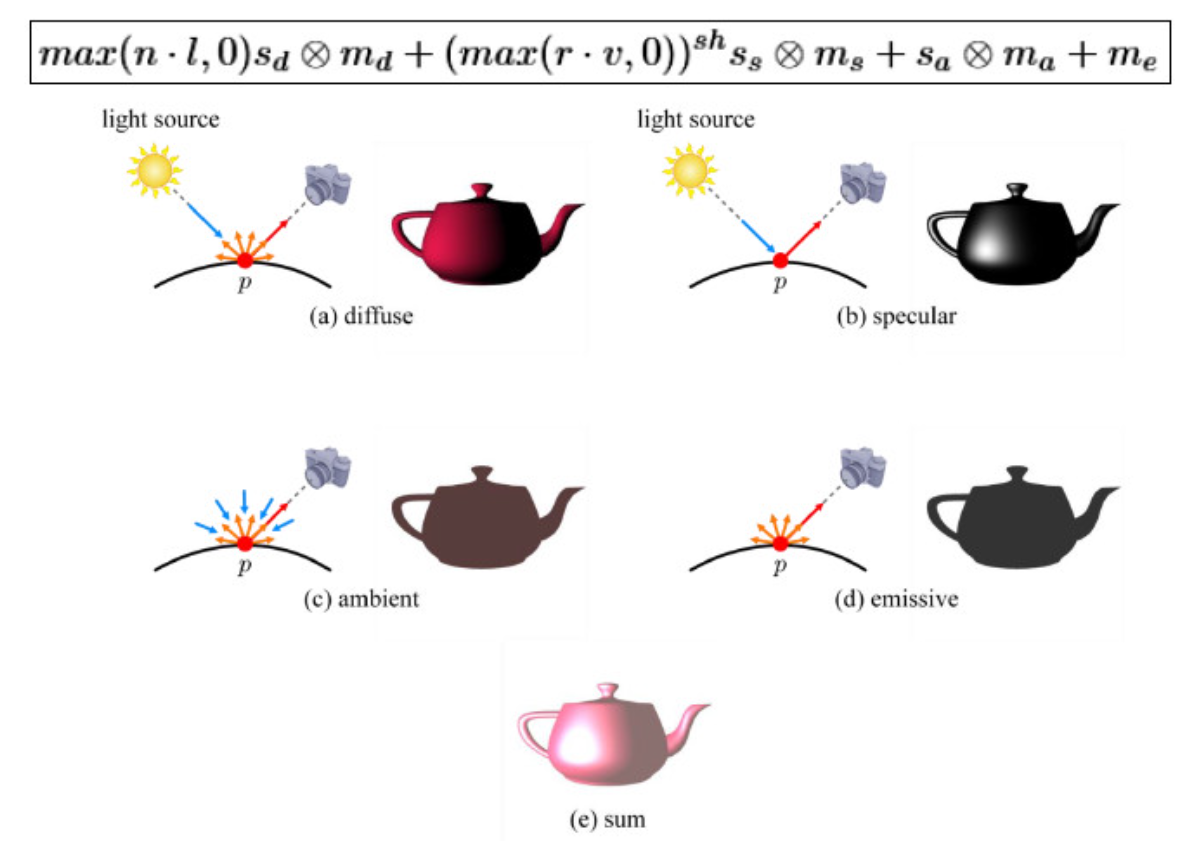
픽셀 셰이더는 입력받은 데이터를 조합하여 조명 모델을 계산한다. 전통적인 퐁(Phong) 또는 블린-퐁(Blinn-Phong) 모델은
다음 네 가지 구성 요소의 합이다.
3.1. Diffuse Light - 난반사
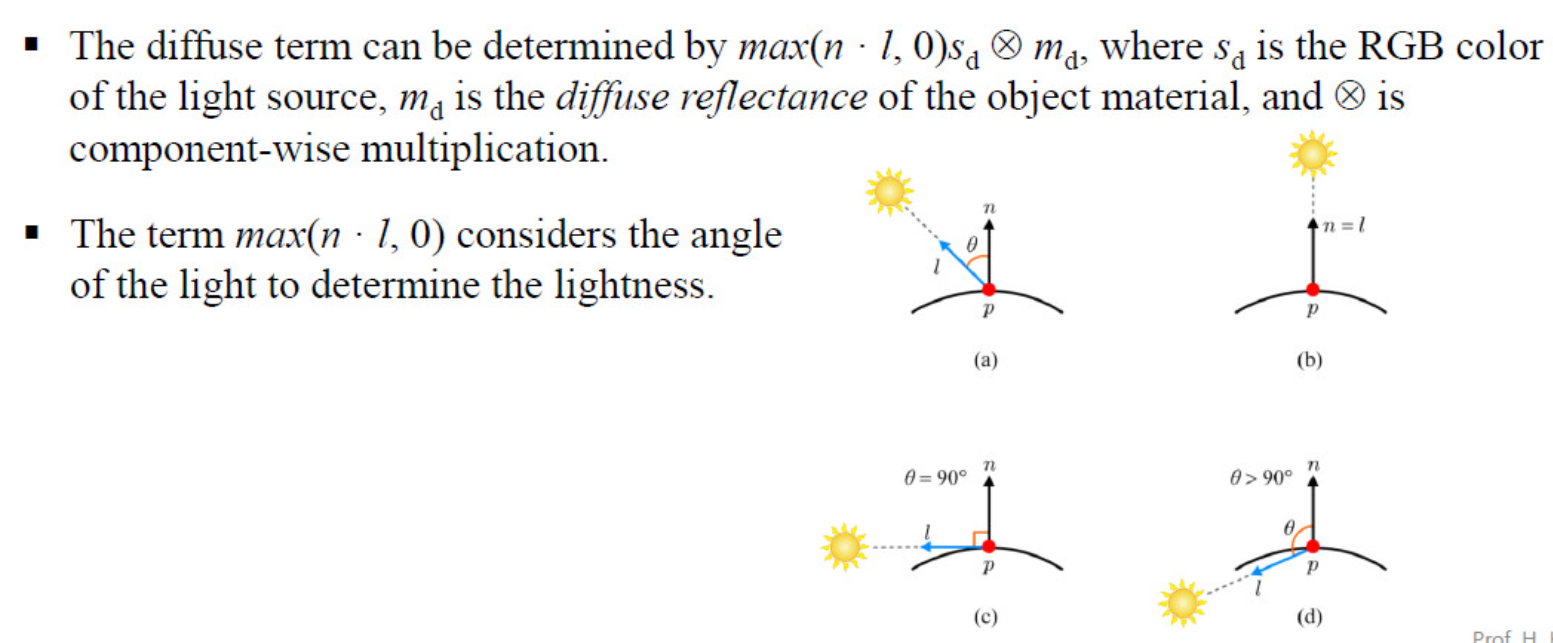

- 광원이 표면에 부딪혀 여러 방향으로 흩어지는 '무광' 반사이다.
- 빛은 균일하게 분포된다.
- PHone Model에서는 Lambert 법칙에 기반을 두고 있으며, 이는 이상적인 diffuse 표면에서의 반사가 모든 방향으로 동일한 강도로 산란된다고 사정한다. 따라서 반사의 양은 View 방향과 무관하며, 들어오는 빛의 양에 비례한다.
3.2. Specular Light - 정반사
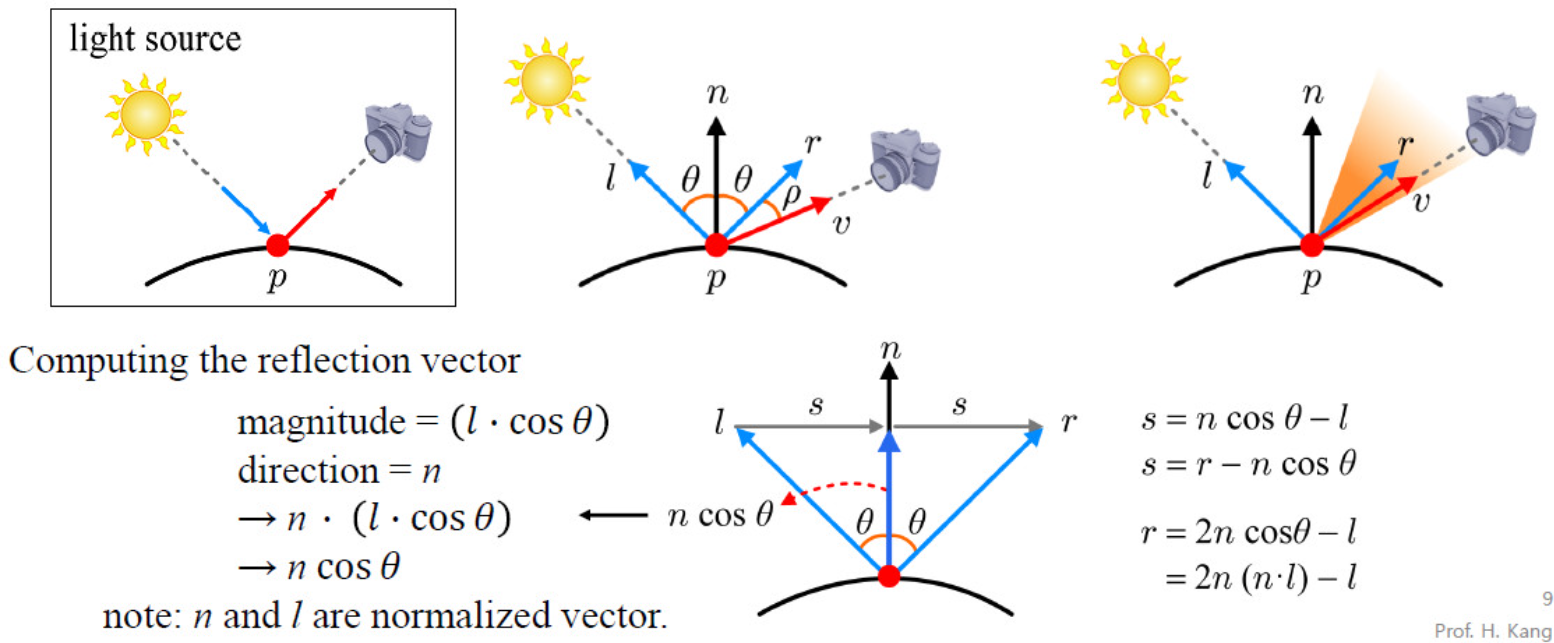
- 광원이 표면에 부딪혀 특정 방향으로 강하게 반사되는 '하이라이트'이다.
- 시선 벡터(V)와 광원의 반사 벡터(R)를 사용하거나, 더 효율적인 블린-퐁(Blinn-Phong) 모델에서는 하프웨이 벡터(H)를 사용한다.
- H = normalize(L + V)

- 하이라이트의 집중도는 재질의 '광택(Shininess, sh)' 값으로 제어한다.
- Specular_Factor = pow(saturate(dot(N, H)), Shininess)
3.3. Ambient Light

- 간접광(Indirect Light) 또는 환경광을 나타내는 가장 기초적인 조명이다.
- 장면의 다양한 객체에서 반사된 빛을 표현한다.
- 이는 장면 내에서 여러 반 반사되기 때문에 표면 모든 지점에 모든 방향에서 도달하며, 표면 지점에서의 반사도 모든 방향으로 동일한 강도로 산란된다.
3.4. Emissive
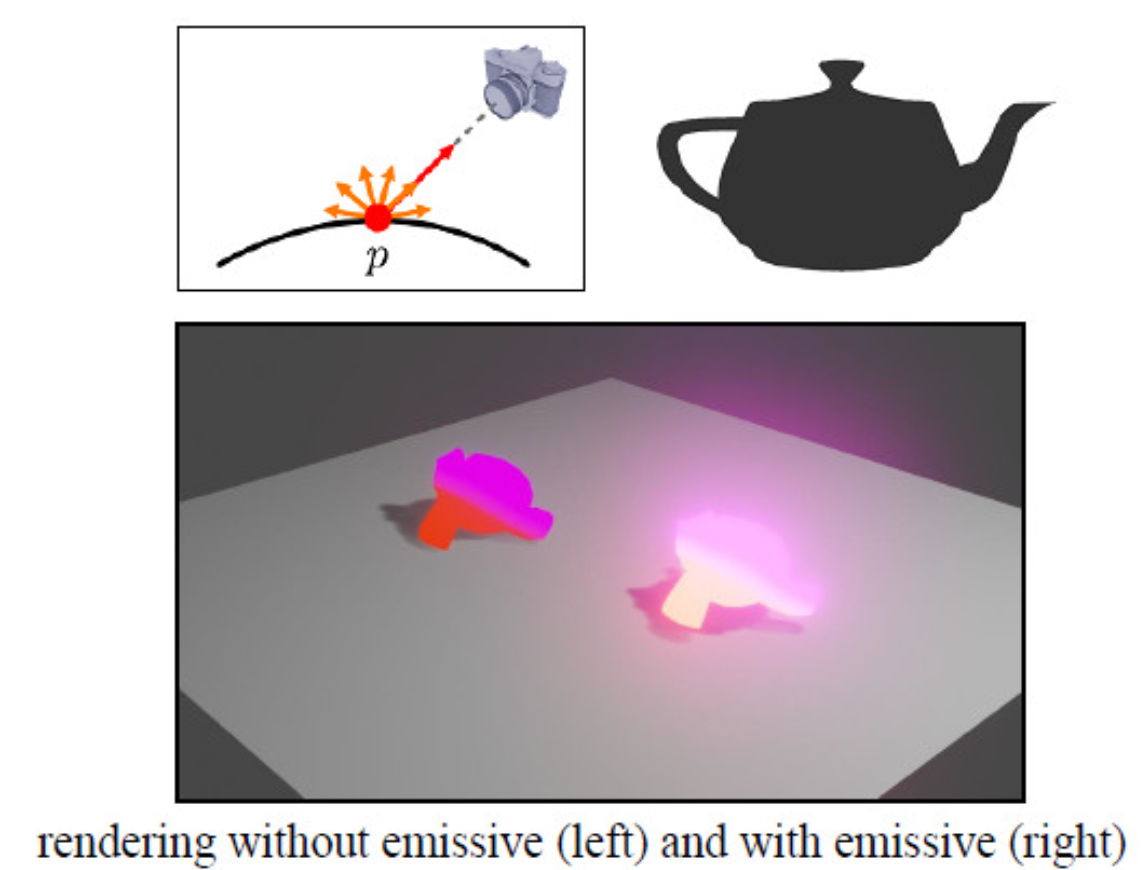
- Emmisive Term은 표면 자체에서 방출되는 빛의 양을 설명한다.
4. 픽셀 단위 조명 (Per-Pixel Lighting)
픽셀 단위 조명(Per-Pixel Lighting)은 3D 렌더링에서 고품질의 사실적인 음영을 구현하기 위한 표준 조명 계산 방식이다. (현대 렌더링에서는 '퐁 셰이딩' 또는 PBR의 기반이 된다.)
이는 조명 계산을 VS에서 수행하는 '정점 단위 조명(Per-Vertex Lighting)'과 다르다.
정점 단위 조명은 정점에서 계산된 '색상(Color)'을 RS가 보간하기 때문에, 폴리곤 표면 전체의 디테일이 낮고 스페큘러(Specular) 하이라이트가 뭉개지는 품질적 한계가 명확하다.
픽셀 단위 조명은 이와 달리, 조명 계산에 필요한 벡터 데이터를 보간하고, PS가 화면의 모든 픽셀(프래그먼트)마다 개별적으로 조명 계산을 수행한다.
4.1. 픽셀 단위 조명의 작동 원리
픽셀 단위 조명은 파이프라인 스테이지 간의 명확한 역할 분담을 통해 이루어진다.
- 정점 셰이더 (VS):
- 조명 계산을 수행하지 않는다.
- 대신, 조명 계산에 필요한 '재료'가 되는 벡터 데이터(예: 법선 벡터 N, 시선 벡터 V, 광원 벡터 L, 탄젠트 벡터 T 등)를 계산하고 준비한다.
- 이 재료들을 다음 단계인 RS로 전달한다.
- 래스터라이저 (RS):
- 삼각형의 꼭짓점 3개로부터 이 '재료' 벡터들을 입력받는다.
- 삼각형 내부를 채우는 모든 프래그먼트(픽셀 후보)에 대해, 이 벡터 값들을 원근 보정 보간(Perspective-Correct Interpolation)한다.
- 픽셀 셰이더 (PS):
- 래스터라이저로부터 픽셀마다 보간된 벡터 값들을 입력받는다.
- 이 재료들(예: n, l, v)과 상수 버퍼(광원 정보)를 이용해, 모든 픽셀에 대해 앰비언트(Ambient), 디퓨즈(Diffuse), 스페큘러(Specular) 등 완전한 조명 계산을 수행한다.
- 이 방식은 픽셀마다 법선이 달라지는 노멀 매핑(Normal Mapping)을 구현하기 위한 필수 전제 조건이다.
4.2. 좌표 공간 통일
조명 계산의 핵심인 내적(Dot Product) 연산(예: dot(N, L))은 모든 벡터가 동일한 좌표 공간에 있어야 한다.
따라서 셰이더는 N, L, V 벡터를 하나의 공간으로 통일해야 한다. 렌더링 방식에 따라 어떤 공간에서 통일 시켜야 하는지 알아봐야 한다. (이는 조사 및 공부가 더 필요)
4.3. 사례 1: 표준 렌더링 (노멀 매핑 X)
- 계산 공간: 월드 공간 (World Space)
- 이유: 이 방식이 연산 비용이 가장 저렴하기 때문이다.
1. 광원 벡터 (L)
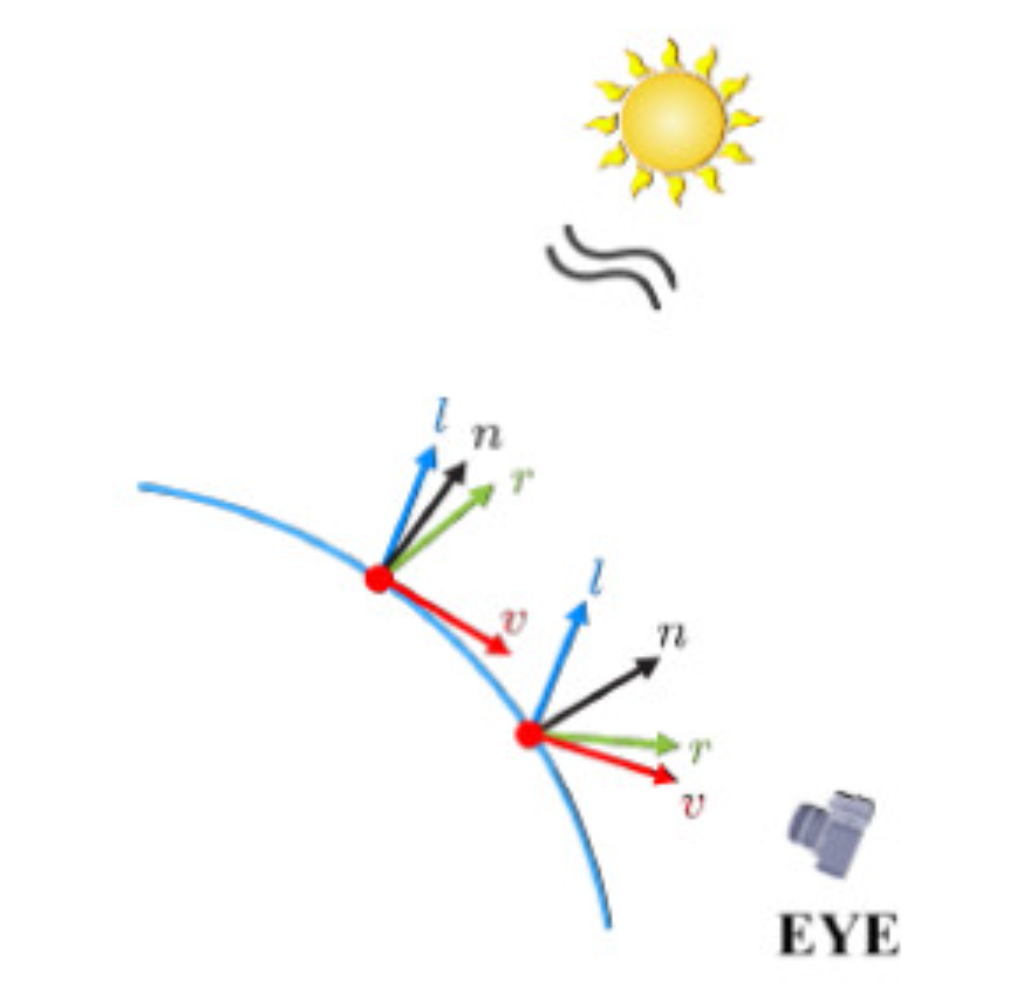
- CPU가 상수 버퍼(Constant Buffer)를 통해 월드 공간 광원 정보(L_world)를 PS에 직접 전달한다. (L은 Directiona Light이기 때문에, 모든 픽셀에 대해 상수(Constant)로 동일하다)
- 각 Pixel Shader 실행에 대해 개별적인 n, v가 필요하고 이를 이용해 r을 계산한다. (r = 2n dot (n, l) - l)
2. 법선 벡터 (N)

- VS: 3D 모델의 정점 법선(N_model)을 World Space로 변환한다.
- RS: World Space에서의 Vertex normal을 보간하여 각 픽셀에 normal을 할당한다.
- PS: 보간된 월드 공간 법선을 입력받는다.
3. View 벡터 (V)

- VS: 정점 위치를 World Space으로 변환한 뒤, 카메라 위치(Eye_world)와의 차이로 월드 공간 시선 벡터(V_world)를 계산한다. (V = Eye - P)
- RS: World Space View 벡터를 픽셀마다 보간한다.
- PS: 보간된 World Space View 벡터를 입력받는다.
4. 픽셀 색상 결정

- 픽셀 쉐이더에 전달된 World space에서 정의된 n과 v, l을 바탕으로, 픽셀 쉐이더는 먼저 Reflection 벡터를 계산한다. 즉, r=2n(n·l)-l을 계산하고 최종적으로 Phong 모델을 구현합니다.
- 단 Pixel Shader의 경우 Smooth한 빛 표현에서는 유리하나, 각 진 Surface나 빛표현에서 약점을 가진다. (Vertex에서 보간을 하기 때문에)
- 이때문에 정점 2개가 겹쳐 보간 됐을 때, 부드럽게 못하는 우회방법이쓰이기도 함. (추후 조사 필요)
4.4. 사례 2: 노멀 매핑 (Normal Mapping O) (추후 조사 필요)
- 계산 공간: 탄젠트 공간 (Tangent Space)
- 이유: 이 방식이 연산 비용이 가장 저렴하기 때문이다.
1. 법선 벡터 (N)
- PS: N 벡터는 더 이상 정점에서 오지 않는다. 픽셀 셰이더가 노멀 맵 텍스처를 샘플링하여 직접 얻어온다.
- 핵심: 이 텍스처에 저장된 법선 데이터는 탄젠트 공간을 기준으로 한다.
2. 광원 벡터 (L) 및 시선 벡터 (V)
- 문제: N이 탄젠트 공간에 있으므로, L과 V도 탄젠트 공간으로 변환되어야 한다.
- 비효율적 방법: N_tangent를 PS에서 월드 공간으로 변환한다. (매우 비쌈. 수백만 픽셀 * 행렬 곱셈)
- 효율적 방법 (표준):
- VS: TBN 행렬을 계산한다.
- VS: 상수 버퍼의 월드 공간 L과 V 벡터를 이 TBN 행렬과 곱하여 탄젠트 공간(L_tangent, V_tangent)으로 미리 변환한다.
- RS: 탄젠트 공간 L과 V 벡터를 픽셀마다 보간한다.
결론: PS는 텍스처에서 N_tangent를 읽고, RS로부터 L_tangent와 V_tangent를 전달받는다. 모든 벡터가 탄젠트 공간에서 준비되므로, PS는 즉시 탄젠트 공간에서 조명 계산을 수행한다.
5. Blinn-Phong Reflection Model
반사 모델은 퐁 반사 모델의 수정된 버전.

- 퐁 조명은 조명의 매우 효율적인 근사치이지만, 특정 조건에서는 그 반사 항이 비현실적인 쉐이딩 결과를 나타낸다.
- Refelction term은 (max(r · v, 0)^sh Ss ⊗ ms로 계산된다.
- Dot product 결과 내적의 결과가 음수가 되면 Max에 의해 결과가 0이 된다.
- 이 즉각적인 cut-off는 표면에 경계를 만든다.
- 이 문제를 극복하기 위해, 블린-퐁 모델은 반사 모델을 다르게 접근한다.
Blinn-Phong reflection model에서는 reflection term이 반사 벡터가 아닌 harfway vector (h)에 의해 계산된다.

6. 최종 출력
픽셀 셰이더는 앰비언트, 디퓨즈, 스페큘러(및 기타 효과) 계산을 모두 마친 최종 색상 값을 SV_Target 시맨틱(Semantic)에 담아 출력한다. 이 값은 파이프라인의 다음 단계인 **출력 병합기(Output Merger)**로 전달된다.
'그래픽스' 카테고리의 다른 글
| 09. Output Merger (0) | 2025.11.05 |
|---|---|
| 08. Pixel Shader - Alpha test (0) | 2025.11.05 |
| 08. Pixel Shader - Normal Mapping (0) | 2025.11.04 |
| 08. Pixel Shader - Image Texturing (0) | 2025.11.04 |
| 07. Rasterizer (0) | 2025.11.04 |
